Fine Tuning LLM: Parameter Efficient Fine Tuning (PEFT), LoRA and QLoRA: Part 1

In the ever-evolving world of AI and Natural Language Processing (NLP), Large Language Models and Generative AI have become powerful tools for various applications. Achieving the desired results from these models involves different approaches that can be broadly classified into three categories: Prompt Engineering, Fine-Tuning, and Creating a new model. As we progress from one level to another, the requirements in terms of resources and costs increase significantly.

In this blog post, we’ll explore these approaches and focus on an efficient technique known as Parameter Efficient Fine-Tuning (PEFT) that allows us to fine-tune models with minimal infrastructure while maintaining high performance.

Prompt Engineering with Existing Models

At the basic level, achieving expected outcomes from Large Language Models involves careful prompt engineering. This process involves crafting suitable prompts and inputs to elicit the desired responses from the model. Prompt Engineering is an essential technique for various use cases, especially when general responses suffice.

Creating a New Model

At the highest level, Creating a new model involves training a model from scratch, specifically tailored for a particular task or domain. This approach provides the highest level of customization, but it demands substantial computational power, extensive data, and time.

Fine Tuning Existing Models

When dealing with domain-specific use cases that require model adaptations, fine-tuning becomes essential. Fine-tuning allows us to leverage existing pre-trained foundation models and adapt them to specific tasks or domains. By training the model on domain-specific data, we can tailor it to perform well on targeted tasks.

However, this process can be resource-intensive and costly, as we will be modifying all the millions of parameters as part of training. Fine-tuning the model requires a lot of training data, a huge infrastructure, and effort.

In the process of full fine-tuning of LLMs, there is a risk of catastrophic forgetting, where previously acquired knowledge from pretraining is lost.

Applying complete fine-tuning to a single model for different domain-specific tasks often results in creating large models tailored to specific tasks, lacking modularity. What we require is a modular approach that avoids altering all parameters while demanding fewer infrastructure resources and less data.

There are various techniques, such as Parameter Efficient Fine Tuning (PEFT), which provide a way to perform modular fine-tuning with optimal resources and cost.

Parameter Efficient Fine Tuning (PEFT)

PEFT is a technique designed to fine-tune models while minimizing the need for extensive resources and cost. PEFT is a great choice when dealing with domain-specific tasks that necessitate model adaptation. By employing PEFT, we can strike a balance between retaining valuable knowledge from the pre-trained model and adapting it effectively to the target task with fewer parameters. There are various ways of achieving Parameter efficient fine-tuning. Low-Rank Parameter or LoRA and QLoRA are the most widely used and effective.

Low-Rank Parameters

This is one of the most widely used methods, where a set of parameters are modularly added to the network with lower dimensional space. Instead of modifying the whole network, only these modular low-rank network is modified to achieve the results.

Let's deep dive into one of the most popular techniques called LoRA and QLoRA

Low-Rank Adaptation (LoRA)

Low-Rank Adaptation provides the modular approach towards fine-tuning a model for domain-specific tasks and provides the capability of transfer learning. LoRA technique can be implemented with fewer resources and is memory efficient.

In the following picture, you can see the dimension/rank decomposition, which reduces the memory footprint considerably.

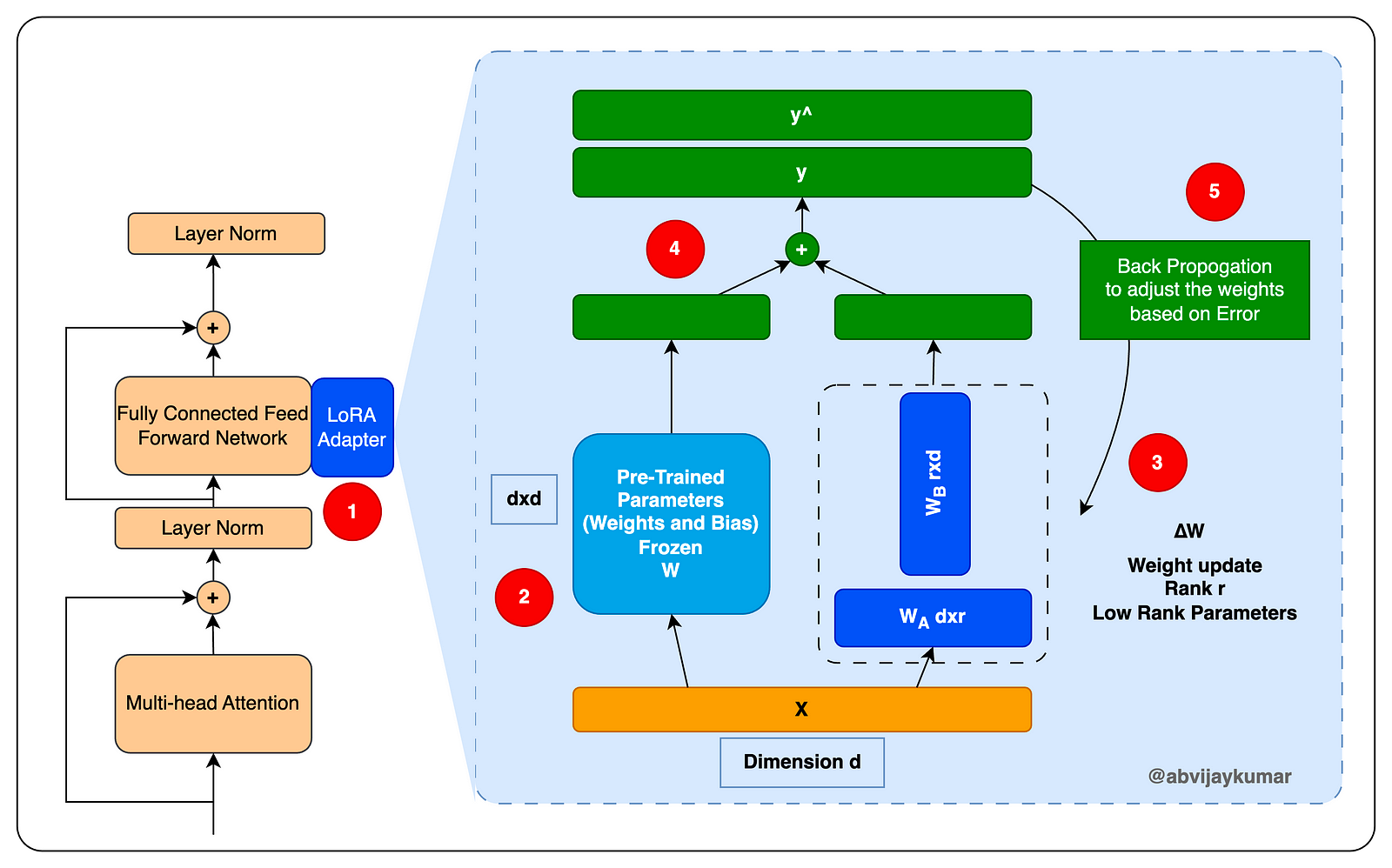
• LoRA can be implemented as an adapter designed to enhance and expand the existing neural network layers. It introduces an additional layer of trainable parameters (weights) while maintaining the original parameters in a frozen state. These trainable parameters possess a substantially reduced rank (dimension) compared to the dimensions of the original network. This is the mechanism through which LoRa simplifies and expedites the process of adapting the original models for domain-specific tasks. Now, let’s take a closer look at the components within the LORA adapter network.
• The pre-trained parameters of the original model (W) are frozen. During training, these weights will not be modified.
• A new set of parameters is concurrently added to the networks WA and WB. These networks utilize low-rank weight vectors, where the dimensions of these vectors are represented as dxr and rxd. Here, ‘d’ stands for the dimension of the original frozen network parameters vector, while ‘r’ signifies the chosen low-rank or lower dimension. The value of ‘r’ is always smaller, and the smaller the ‘r’, the more expedited and simplified the model training process becomes. Determining the appropriate value for ‘r’ is a pivotal decision in LoRA. Opting for a lower value results in faster and more cost-effective model training, though it may not yield optimal results. Conversely, selecting a higher value for ‘r’ extends the training time and cost but enhances the model’s capability to handle more complex tasks.
• The results of the original network and the low-rank network are computed with a dot product, which results in a weight matrix of n dimension, which is used to generate the result.
• This result is then compared with the expected results (during training) to calculate the loss function, and WA and WB weights are adjusted based on the loss function as part of backpropagation like standard neural networks.

Let’s explore how this approach contributes to the reduction of the memory footprint and minimizes infrastructure requirements. Consider a scenario where we have a 512x512 parameter matrix within the feed-forward network, amounting to a total of 262,144 parameters that need to undergo training. If we choose to freeze these parameters during the training process and introduce a LoRA adapter with a rank of 2, the outcome is as follows: WA will have 512*2 parameters, and WB will also have 512*2 parameters, summing up to a total of 2,048 parameters. These are the specific parameters that undergo training with domain-specific data. This represents a significant enhancement in computational efficiency, substantially reducing the number of computations required during the backpropagation process. This mechanism is pivotal in achieving accelerated training.

The most advantageous aspect of this approach is that the trained LoRA adapter can be preserved independently and employed as distinct modules. By constructing domain-specific modules in this manner, we effectively achieve a high level of modularity. Additionally, by refraining from altering the original weights, we successfully circumvent the issue of catastrophic forgetting.

Now, let’s delve into further enhancements that can be implemented atop LoRA, particularly through the utilization of QLoRA, in order to elevate the optimization to the next level.

Quantized Low-Ranking Adaptation (QLoRA)

QLoRA extends LoRA to enhance efficiency by quantizing weight values of the original network, from high-resolution data types, such as Float32, to lower-resolution data types like int4. This leads to reduced memory demands and faster calculations.

There are three Key optimizations that QLoRA brings on top of LoRA, which makes QLoRA one of the best PEFT methods.

4-bit NF4 Quantization

4-bit NormalFloat4 is an optimized data type that can be used to store weights, which brings down the memory footprint considerably. 4-bit NormalFloat4 quantization is a 3-step process.

• Normalization and Quantization: As part of normalization and quantization steps, the weights are adjusted to a zero mean and a constant unit variance. A 4-bit data type can only store 16 numbers. As part of normalization, the weights are mapped to these 16 numbers, zero-centered distributed, and instead of storing the weights, the nearest position is stored. Here is an example

Let's say we have a FP32 weight with a value of 0.2121. a 4-bit split between -1 to 1 will be the following number positions.

0.2121 is closest to 0.1997, which is the 10th position. Instead of saving the FP32 of 0.2121, we store 10.

The typical formula:

int4Tensor = roundedValue(totalNumberOfPositions/absmax(inputXTensor)) 
                    * FP32WeightsTensor

In the above example 
totalNumberOfPositions = 16

The value totalNumberOfPositions/absmax(inputXTensor) is called the quantization constant

Obviously, there is a loss of data when we normalize and quantize as we move from FP32, which is a high-resolution data type, to a low-resolution data type. The loss is not huge as long as there are no outliers in the input tensor, which might affect the absmax () and eventually upset the distribution. To avoid that issue, we generally quantize the weights independently by smaller blocks, which will normalize the outliers.

• Dequantization: To Dequantize the values, we do exactly the reverse.

dequantizedTensor = int4Tensor
                     /roundedValue(totalNumberOfPositions/absmax(inputXTensor))

In the above example 
totalNumberOfPositions = 16

The 4-bit NormalFloat quantization is applied to the weights of the original model; the LoRA adapter weights will be FP32, as all of the training will happen on these weights. Once all the training is done, the original weights will be de-quantized.

Double Quantization

Double quantization further reduces the memory footprint by quantizing quantization constants. In the previous 4-bit FP4 quantization step, we calculated the quantization constant. Even that can be quantized for better efficiency, and that is what we do in Double Quantization.

Since the quantization is done in blocks, to avoid outliers, typically 64 weights in 1 block, we will have one quantization constant. These quantization constants can be quantized further to reduce the memory footprint.

Let's say we have grouped 64 parameters/weights per block, and each quantization constant takes 32 bits, as it is FP32. It adds a 0.5 bit per parameter on average, which means we are talking of at least 500,000 bits for a typical 1Mil parameter model.

With Double quantization, we apply quantization on these quantization constants, which will further optimize our memory usage. We can take a group of 256 quantization values and apply 8-bit quantization. we can achieve approximately 0.127 bits per parameter, which brings down the value to 125,000 bits for the 1Mil parameter model.

Here is the calculation: We have 64 weights in 256 blocks, which are 32 bits, which is 32/(64*256), which is 0.001953125.

We have 8bits for 64 weights, which is 8/64 0.125.

If we add it up 0.125+0.001953125, which is 0.127 approximately.

Unified Memory Paging

Coupled with the above techniques, QLoRA also utilizes the nVidia unified memory feature, which allows GPU->CPU seamless page transfers when GPU runs out of memory, thus managing the sudden memory spikes in GPU and helping memory overflow/overrun issues.

LoRA and QLoRA are two of the most emerging and widely used techniques for Parameter Efficient Fine tuning.

In the next part, we will implement QLoRA; until then, have fun with LLMs.

Hope this was useful; leave your comments and feedback...

Bye for now...