Covers machine learning for predictive analytics, explains setting up training and testing data, and offers machine learning model snippets.
Written By
Predictive Analytics is about predicting future outcome based on analyzing data collected previously. It includes two phases:
We can choose many models, each based on a set of different assumptions regarding the underlying distribution of data. Therefore, we are interested in two general types of problems in this discussion: 1. Classification—about predicting a category (a value that is discrete, finite with no ordering implied), and 2. Regression—about predicting a numeric quantity (a value that's continuous and infinite with ordering).
For classification problems, we use the "iris" data set and predict its "species" from its "width" and "length" measures of sepals and petals. Here is how we set up our training and testing data:
> summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300000 Min. :2.000000 Min. :1.000 Min. :0.100000
1st Qu.:5.100000 1st Qu.:2.800000 1st Qu.:1.600 1st Qu.:0.300000
Median :5.800000 Median :3.000000 Median :4.350 Median :1.300000
Mean :5.843333 Mean :3.057333 Mean :3.758 Mean :1.199333
3rd Qu.:6.400000 3rd Qu.:3.300000 3rd Qu.:5.100 3rd Qu.:1.800000
Max. :7.900000 Max. :4.400000 Max. :6.900 Max. :2.500000
Species
setosa :50
versicolor:50
virginica :50
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
>
> # Prepare training and testing data
> testidx <- which(1:length(iris[,1])%%5 == 0)
> iristrain <- iris[-testidx,]
> iristest <- iris[testidx,]
To illustrate a regression problem (where the output we predict is a numeric quantity), we'll use the "Prestige" data set imported from the "car" package to create our training and testing data.
> library(car)
> summary(Prestige)
education income women
Min. : 6.38000 Min. : 611.000 Min. : 0.00000
1st Qu.: 8.44500 1st Qu.: 4106.000 1st Qu.: 3.59250
Median :10.54000 Median : 5930.500 Median :13.60000
Mean :10.73804 Mean : 6797.902 Mean :28.97902
3rd Qu.:12.64750 3rd Qu.: 8187.250 3rd Qu.:52.20250
Max. :15.97000 Max. :25879.000 Max. :97.51000
prestige census type
Min. :14.80000 Min. :1113.000 bc :44
1st Qu.:35.22500 1st Qu.:3120.500 prof:31
Median :43.60000 Median :5135.000 wc :23
Mean :46.83333 Mean :5401.775 NA's: 4
3rd Qu.:59.27500 3rd Qu.:8312.500
Max. :87.20000 Max. :9517.000
> head(Prestige)
education income women prestige census type
gov.administrators 13.11 12351 11.16 68.8 1113 prof
general.managers 12.26 25879 4.02 69.1 1130 prof
accountants 12.77 9271 15.70 63.4 1171 prof
purchasing.officers 11.42 8865 9.11 56.8 1175 prof
chemists 14.62 8403 11.68 73.5 2111 prof
physicists 15.64 11030 5.13 77.6 2113 prof
> testidx <- which(1:nrow(Prestige)%%4==0)
> prestige_train <- Prestige[-testidx,]
> prestige_test <- Prestige[testidx,]
Linear regression has the longest, most well-understood history in statistics, and is the most popular machine learning model. It is based on the assumption that a linear relationship exists between the input and output variables, as follows:
y = Ө0 + Ө1x1 + Ө 2x2 + …
…where y is the output numeric value, and xi is the input numeric value.
The learning algorithm will learn the set of parameters such that the sum of square error (yactual - yestimate)2 is minimized. Here is the sample code that uses the R language to predict the output "prestige" from a set of input variables:
> model <- lm(prestige~., data=prestige_train)
> # Use the model to predict the output of test data
> prediction <- predict(model, newdata=prestige_test)
> # Check for the correlation with actual result
> cor(prediction, prestige_test$prestige)
[1] 0.9376719009
> summary(model)
Call:
lm(formula = prestige ~ ., data = prestige_train)
Residuals:
Min 1Q Median 3Q Max
-13.9078951 -5.0335742 0.3158978 5.3830764 17.8851752
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -20.7073113585 11.4213272697 -1.81304 0.0743733 .
education 4.2010288017 0.8290800388 5.06710 0.0000034862 ***
income 0.0011503739 0.0003510866 3.27661 0.0016769 **
women 0.0363017610 0.0400627159 0.90612 0.3681668
census 0.0018644881 0.0009913473 1.88076 0.0644172 .
typeprof 11.3129416488 7.3932217287 1.53018 0.1307520
typewc 1.9873305448 4.9579992452 0.40083 0.6898376
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.41604 on 66 degrees of freedom
(4 observations deleted due to missingness)
Multiple R-squared: 0.820444, Adjusted R-squared: 0.8041207
F-statistic: 50.26222 on 6 and 66 DF, p-value: < 0.00000000000000022204
The coefficient column gives an estimation of Өi, and an associated p-value gives the confidence of each estimated Өi. For example, features not marked with at least one * can be safely ignored.
In the above model, education and income has a high influence to the prestige.
The goal of minimizing the square error makes linear regression very sensitive to outliers that greatly deviate in the output. It is a common practice to identify those outliers, remove them, and then rerun the training.
Among all, the value against support column indicates whether an engine can be used or not.
In a classification problem, the output is binary rather than numeric. We can imagine doing a linear regression and then compressing the numeric output into a 0..1 range using the logit function 1/(1+e-t), shown here:
y = 1/(1 + e -(Ɵ0+ Ɵ1x1 +Ɵ2x2+ …))
…where y is the 0 .. 1 value, and xi is the input numeric value.
The learning algorithm will learn the set of parameters such that the cost (yactual * log yestimate + (1 - yactual) * log(1 - yestimate)) is minimized.
Here is the sample code that uses the R language to perform a binary classification using iris data.
> newcol = data.frame(isSetosa=(iristrain$Species == 'setosa'))
> traindata <- cbind(iristrain, newcol)
> head(traindata)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species isSetosa
1 5.1 3.5 1.4 0.2 setosa TRUE
2 4.9 3.0 1.4 0.2 setosa TRUE
3 4.7 3.2 1.3 0.2 setosa TRUE
4 4.6 3.1 1.5 0.2 setosa TRUE
6 5.4 3.9 1.7 0.4 setosa TRUE
7 4.6 3.4 1.4 0.3 setosa TRUE
> formula <- isSetosa ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
> logisticModel <- glm(formula, data=traindata, family="binomial")
Warning messages:
1: glm.fit: algorithm did not converge
2: glm.fit: fitted probabilities numerically 0 or 1 occurred
> # Predict the probability for test data
> prob <- predict(logisticModel, newdata=iristest, type='response')
> round(prob, 3)
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
105 110 115 120 125 130 135 140 145 150
0 0 0 0 0 0 0 0 0 0
To avoid an over-fitting problem (the trained model fits too well with the training data and is not generalized enough), the regularization technique is used to shrink the magnitude of Ɵi. This is done by adding a penalty (a function of the sum of Ɵi) into the cost function.
In L2 regularization (also known as Ridge regression), Ɵi2 will be added to the cost function. In L1 regularization (also known as Lasso regression), ||Ɵi|| will be added to the cost function. Both L1, L2 will shrink the magnitude of Ɵi. For variables that are inter-dependent, L2 tends to spread the shrinkage such that all interdependent variables are equally influential. On the other hand, L1 tends to keep one variable and shrink all the other dependent variables to values very close to zero. In other words, L1 shrinks the variables in an uneven manner so that it can also be used to select input variables.
Combining L1 and L2, the general form of the cost function becomes the following:
Cost == Non-regularization-cost + λ (α.Σ ||Ɵi|| + (1- α).Σ Ɵi2)
Notice the 2 tunable parameters, lambda, λ, and alpha, α. Lambda controls the degree of regularization (0 means no regularization and infinity means ignoring all input variables because all coefficients of them will be zero). Alpha controls the degree of mix between L1 and L2 (0 means pure L2 and 1 means pure L1). Glmnet is a popular regularization package. The alpha parameter needs to be supplied based on the application's need, i.e., its need for selecting a reduced set of variables. Alpha=1 is preferred. The library provides a cross-validation test to automatically choose the better lambda value. Let's repeat the above linear regression example and use regularization this time. We pick alpha = 0.7 to favor L1 regularization.
> library(glmnet)
> cv.fit <- cv.glmnet(as.matrix(prestige_train[,c(-4, -6)]), as.vector(prestige_train[,4]), nlambda=100, alpha=0.7, family="gaussian")
> plot(cv.fit)
> coef(cv.fit)
5 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 6.3876684930151
education 3.2111461944976
income 0.0009473793366
women 0.0000000000000
census 0.0000000000000
> prediction <- predict(cv.fit, newx=as.matrix(prestige_test[,c(-4, -6)]))
> cor(prediction, as.vector(prestige_test[,4]))
[,1]
1 0.9291181193
This is the cross-validation plot. It shows the best lambda with minimal-root,mean-square error.
A Neural Network emulates the structure of a human brain as a network of neurons that are interconnected to each other. Each neuron is technically equivalent to a logistic regression unit.
In this setting, neurons are organized in multiple layers where every neuron at layer i connects to every neuron at layer i+1 and nothing else. The tuning parameters in a neural network include the number of hidden layers (commonly set to 1), the number of neurons in each layer (which should be same for all hidden layers and usually at 1 to 3 times the input variables), and the learning rate. On the other hand, the number of neurons at the output layer depends on how many binary outputs need to be learned. In a classification problem, this is typically the number of possible values at the output category.
The learning happens via an iterative feedback mechanism where the error of training data output is used to adjust the corresponding weights of input. This adjustment propagates to previous layers and the learning algorithm is known as "backpropagation." Here is an example:
> library(neuralnet)
> nnet_iristrain <-iristrain
> #Binarize the categorical output
> nnet_iristrain <- cbind(nnet_iristrain, iristrain$Species == 'setosa')
> nnet_iristrain <- cbind(nnet_iristrain, iristrain$Species == 'versicolor')
> nnet_iristrain <- cbind(nnet_iristrain, iristrain$Species == 'virginica')
> names(nnet_iristrain)[6] <- 'setosa'
> names(nnet_iristrain)[7] <- 'versicolor'
> names(nnet_iristrain)[8] <- 'virginica'
> nn <- neuralnet(setosa+versicolor+virginica ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data=nnet_iristrain, hidden=c(3))
> plot(nn)
> mypredict <- compute(nn, iristest[-5])$net.result
> # Consolidate multiple binary output back to categorical output
> maxidx <- function(arr) {
+ return(which(arr == max(arr)))
+ }
> idx <- apply(mypredict, c(1), maxidx)
> prediction <- c('setosa', 'versicolor', 'virginica')[idx]
> table(prediction, iristest$Species)
prediction setosa versicolor virginica
setosa 10 0 0
versicolor 0 10 3
virginica 0 0 7
>
Neural networks are very good at learning non-linear functions. They can even learn multiple outputs simultaneously, though the training time is relatively long, which makes the network susceptible to local minimum traps. This can be mitigated by doing multiple rounds and picking the best-learned model.
A Support Vector Machine provides a binary classification mechanism based on finding a hyperplane between a set of samples with +ve and -ve outputs. It assumes the data is linearly separable.
The problem can be structured as a quadratic programming optimization problem that maximizes the margin subjected to a set of linear constraints (i.e., data output on one side of the line must be +ve while the other side must be -ve). This can be solved with the quadratic programming technique.
If the data is not linearly separable due to noise (the majority is still linearly separable), then an error term will be added to penalize the optimization.
If the data distribution is fundamentally non-linear, the trick is to transform the data to a higher dimension so the data will be linearly separable.The optimization term turns out to be a dot product of the transformed points in the high-dimension space, which is found to be equivalent to performing a kernel function in the original (before transformation) space.
The kernel function provides a cheap way to equivalently transform the original point to a high dimension (since we don't actually transform it) and perform the quadratic optimization in that high-dimension space.
There are a couple of tuning parameters (e.g., penalty and cost), so transformation is usually conducted in 2 steps—finding the optimal parameter and then training the SVM model using that parameter. Here are some example codes in R:
parameter. Here are some example codes in R:
> library(e1071)
> tune <- tune.svm(Species~., data=iristrain, gamma=10^(-6:-1), cost=10^(1:4))
> summary(tune)
Parameter tuning of 'svm':
- sampling method: 10-fold cross validation
- best parameters:
gamma cost
0.001 10000
- best performance: 0.03333333
> model <- svm(Species~., data=iristrain, method="C-classification", kernel="radial", probability=T, gamma=0.001, cost=10000)
> prediction <- predict(model, iristest, probability=T)
> table(iristest$Species, prediction)
prediction
setosa versicolor virginica
setosa 10 0 0
versicolor 0 10 0
virginica 0 3 7
>
SVM with a Kernel function is a highly effective model and works well across a wide range of problem sets. Although it is a binary classifier, it can be easily extended to a multi-class classification by training a group of binary classifiers and using "one vs all" or "one vs one" as predictors.
SVM predicts the output based on the distance to the dividing hyperplane. This doesn't directly estimate the probability of the prediction. We therefore use the calibration technique to find a logistic regression model between the distance of the hyperplane and the binary output. Using that regression model, we then get our estimation.
From a probabilistic viewpoint, the predictive problem can be viewed as a conditional probability estimation; trying to find Y where P(Y | X) is maximized.
From the Bayesian rule, P(Y | X) == P(X | Y) * P(Y) / P(X)
This is equivalent to finding Y where P(X | Y) * P(Y) is maximized.
Let's say the input X contains 3 categorical features— X1, X2, X3. In the general case, we assume each variable can potentially influence any other variable. Therefore the joint distribution becomes:
P(X | Y) = P(X1 | Y) * P(X2 | X1, Y) * P(X3 | X1, X2, Y)
P(X | Y) == P(X1 | Y) * P(X2 | Y) * P(X3 | Y), we need to find the Y that maximizes P(X1 | Y) * P(X2 | Y) * P(X3 | Y) * P(Y)
Each term on the right hand side can be learned by counting the training data. Therefore we can estimate P(Y | X) and pick Y to maximize its value.
But it is possible that some patterns never show up in training data, e.g., P(X1=a | Y=y) is 0. To deal with this situation, we pretend to have seen the data of each possible value one more time than we actually have.
P(X1=a | Y=y) == (count(a, y) + 1) / (count(y) + m)
…where m is the number of possible values in X1.
When the input features are numeric, say a = 2.75, we can assume X1 is the normal distribution. Find out the mean and standard deviation of X1 and then estimate P(X1=a) using the normal distribution function.
Here is how we use Naïve Bayes in R:
> library(e1071)
> # Can handle both categorical and numeric input variables, but output must be categorical
> model <- naiveBayes(Species~., data=iristrain)
> prediction <- predict(model, iristest[,-5])
> table(prediction, iristest[,5])
prediction setosa versicolor virginica
setosa 10 0 0
versicolor 0 10 2
virginica 0 0 8
Notice the independence assumption is not true in most cases.Nevertheless, the system still performs incredibly well. Onestrength of Naïve Bayes is that it is highly scalable and can learn incrementally—all we have to do is count the observed variables and update the probability distribution.
A contrast to model-based learning is K-Nearest neighbor. This is also called instance-based learning because it doesn't even learn a single model. The training process involves memorizing all the training data. To predict a new data point, we found the closest K (a tunable parameter) neighbors from the training set and let them vote for the final prediction.
To determine the "nearest neighbors," a distance function needs to be defined (e.g., a Euclidean distance function is a common one for numeric input variables). The voting can also be weighted among the K-neighbors based on their distance from the new data point.
Here is the R code using K-nearest neighbor for classification.
> library(class)
> train_input <- as.matrix(iristrain[,-5])
> train_output <- as.vector(iristrain[,5])
> test_input <- as.matrix(iristest[,-5])
> prediction <- knn(train_input, test_input, train_output, k=5)
> table(prediction, iristest$Species)
prediction setosa versicolor virginica
setosa 10 0 0
versicolor 0 10 1
virginica 0 0 9
>
The strength of K-nearest neighbor is its simplicity. No model needs to be trained. Incremental learning is automatic when more data arrives (and old data can be deleted as well). The weakness of KNN, however, is that it doesn't handle high numbers of dimensions well.
Based on a tree of decision nodes, the learning approach is to recursively divide the training data into buckets of homogeneous members through the most discriminative dividing criteria possible. The measurement of "homogeneity" is based on the output label; when it is a numeric value, the measurement will be the variance of the bucket; when it is a category, the measurement will be the entropy, or "gini index," of the bucket.
During the training, various dividing criteria based on the input will be tried (and used in a greedy manner); when the input is a category (Mon, Tue, Wed, etc.), it will first be turned into binary (isMon, isTue, isWed, etc.,) and then it will use true/false as a decision boundary to evaluate homogeneity; when the input is a numeric or ordinal value, the lessThan/greaterThan at each training-data input value will serve as the decision boundary.
The training process stops when there is no significant gain in homogeneity after further splitting the Tree. The members of the bucket represented at leaf node will vote for the prediction; the majority wins when the output is a category. The member's average is taken when the output is a numeric.
Here is an example in R:
> library(rpart)
> #Train the decision tree
> treemodel <- rpart(Species~., data=iristrain)
> plot(treemodel)
> text(treemodel, use.n=T)
> #Predict using the decision tree
> prediction <- predict(treemodel, newdata=iristest, type='class')
> #Use contingency table to see how accurate it is
> table(prediction, iristest$Species)
prediction setosa versicolor virginica
setosa 10 0 0
versicolor 0 10 3
virginica 0 0 7
> names(nnet_iristrain)[8] <- 'virginica'
Here is the Tree model that has been learned:
T h e g o o d part of the Tree is that it can take different data types of input and output variables that can be categorical, binary and numeric values. It can handle missing attributes and outliers well. Decision Tree is also good in explaining reasoning for its prediction and therefore gives good insight about the underlying data.
The limitation of Decision Tree is that each decision boundary at each split point is a concrete binary decision. Also, the decision criteria considers only one input attribute at a time, not a combination of multiple input variables. Another weakness of Decision Tree is that once learned it cannot be updated incrementally. When new training data arrives, you have to throw away the old tree and retrain all data from scratch. In practice, standalone decision trees are rarely used because their accuracy ispredictive and relatively low . Tree ensembles (described below) are the common way to use decision trees.
Instead of picking a single model, Ensemble Method combines multiple models in a certain way to fit the training data. Here are the two primary ways: "bagging" and "boosting." In "bagging", we take a subset of training data (pick n random sample out of N training data, with replacement) to train up each model. After multiple models are trained, we use a voting scheme to predict future data.
Random Forest is one of the most popular bagging models; in addition to selecting n training data out of N at each decision node of the tree, it randomly selects m input features from the total M input features (m ~ M^0.5). Then it learns a decision tree from that. Finally, each tree in the forest votes for the result. Here is the R code to use Random Forest:
> library(randomForest)
#Train 100 trees, random selected attributes
> model <- randomForest(Species~., data=iristrain, nTree=500)
#Predict using the forest
> prediction <- predict(model, newdata=iristest, type='class')
> table(prediction, iristest$Species)
> importance(model)
MeanDecreaseGini
Sepal.Length 7.807602
Sepal.Width 1.677239
Petal.Length 31.145822
Petal.Width 38.617223
"Boosting" is another approach in Ensemble Method. Instead of sampling the input features, it samples the training data records. It puts more emphasis, though, on the training data that is wrongly predicted in previous iterations. Initially, each training data is equally weighted. At each iteration, the data that is wrongly classified will have its weight increased.
Gradient Boosting Method is one of the most popular boosting methods. It is based on incrementally adding a function that fits the residuals.
Set i = 0 at the beginning, and repeat until convergence.
Below is Gradient-Boosted Tree using the decision tree as the learning model F. Here is the sample code in R:
> library(gbm)
> iris2 <- iris
> newcol = data.frame(isVersicolor=(iris2$Species=='versicolor'))
> iris2 <- cbind(iris2, newcol)
> iris2[45:55,]
Sepal.Length Sepal.Width Petal.Length Petal.Width Species isVersicolor
45 5.1 3.8 1.9 0.4 setosa FALSE
46 4.8 3.0 1.4 0.3 setosa FALSE
47 5.1 3.8 1.6 0.2 setosa FALSE
48 4.6 3.2 1.4 0.2 setosa FALSE
49 5.3 3.7 1.5 0.2 setosa FALSE
50 5.0 3.3 1.4 0.2 setosa FALSE
51 7.0 3.2 4.7 1.4 versicolor TRUE
52 6.4 3.2 4.5 1.5 versicolor TRUE
53 6.9 3.1 4.9 1.5 versicolor TRUE
54 5.5 2.3 4.0 1.3 versicolor TRUE
55 6.5 2.8 4.6 1.5 versicolor TRUE
> formula <- isVersicolor ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
> model <- gbm(formula, data=iris2, n.trees=1000, interaction.depth=2, distribution="bernoulli")
Iter TrainDeviance ValidDeviance StepSize Improve
1 1.2714 -1.#IND 0.0010 0.0008
2 1.2705 -1.#IND 0.0010 0.0004
3 1.2688 -1.#IND 0.0010 0.0007
4 1.2671 -1.#IND 0.0010 0.0008
5 1.2655 -1.#IND 0.0010 0.0008
6 1.2639 -1.#IND 0.0010 0.0007
7 1.2621 -1.#IND 0.0010 0.0008
8 1.2614 -1.#IND 0.0010 0.0003
9 1.2597 -1.#IND 0.0010 0.0008
10 1.2580 -1.#IND 0.0010 0.0008
100 1.1295 -1.#IND 0.0010 0.0008
200 1.0090 -1.#IND 0.0010 0.0005
300 0.9089 -1.#IND 0.0010 0.0005
400 0.8241 -1.#IND 0.0010 0.0004
500 0.7513 -1.#IND 0.0010 0.0004
600 0.6853 -1.#IND 0.0010 0.0003
700 0.6266 -1.#IND 0.0010 0.0003
800 0.5755 -1.#IND 0.0010 0.0002
900 0.5302 -1.#IND 0.0010 0.0002
1000 0.4901 -1.#IND 0.0010 0.0002
> prediction <- predict.gbm(model, iris2[45:55,], type="response", n.trees=1000)
> round(prediction, 3)
[1] 0.127 0.131 0.127 0.127 0.127 0.127 0.687 0.688 0.572 0.734 0.722
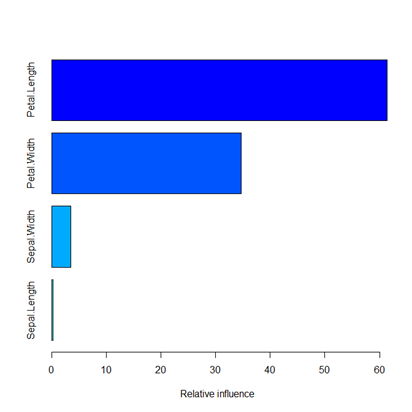
> summary(model)
var rel.inf
1 Petal.Length 61.4203761582
2 Petal.Width 34.7557511871
3 Sepal.Width 3.5407662531
4 Sepal.Length 0.2831064016
The GBM R package also gave the relative importance of the input features, as shown in the bar graph.
{{ parent.title || parent.header.title}}
{{ parent.tldr }}
{{ parent.linkDescription }}
{{ parent.urlSource.name }}