Navigating Vector Databases and Search Through the Prism of Colors

Vector technology in AI, often referred to with implementations, vector indexes, and vector search, offers a robust mechanism index and query through high-dimensional data entities spanning images, text, audio, and video. Their prowess becomes evident across diverse spectrums like similarity-driven searches, multi-modal retrieval, dynamic recommendation engines, and platforms leveraging the Retrieval Augmented Generation (RAG) paradigm. Due to its potential impact on a multitude of use cases, vectors have emerged as a hot topic. As one delves deeper, attempting to demystify the essence of "what precisely is vector search?", they are often greeted by a barrage of terms — AI, LLM, generative AI — to name a few. This article aims to paint a clearer picture (quite literally) by likening the concept to something we all know: colors.

Infinite hues bloom,

A million shades dance and play,

Colors light our world.

Just the so-called "official colors" span across three long Wikipedia pages. While it's straightforward to store and search these colors by their names using conventional search indices like those in Elastic Search or Couchbase FTS, there's a hitch. Think about the colors Navy and Ocean. Intuitively, they feel closely related, evoking images of deep, serene waters. Yet, linguistically, they share no common ground. This is where traditional search engines hit a wall.

The typical workaround? Synonyms. You could map Navy to a plethora of related terms: blue, azure, ocean, turquoise, sky, and so on. But now, consider the gargantuan task of doing this for every color name. Moreover, these lists don't give us a measure of the closeness between colors. Is azure closer to the navy than the sky? A list won't tell you that. To put it simply, seeking similarities among colors is a daunting task. Trying to craft relationships between colors to gauge their similarity? Even more challenging.

The simple solution to this is the well-known RGB. Encoding colors in the RGB vector scheme solves both the similarity and distance problem.

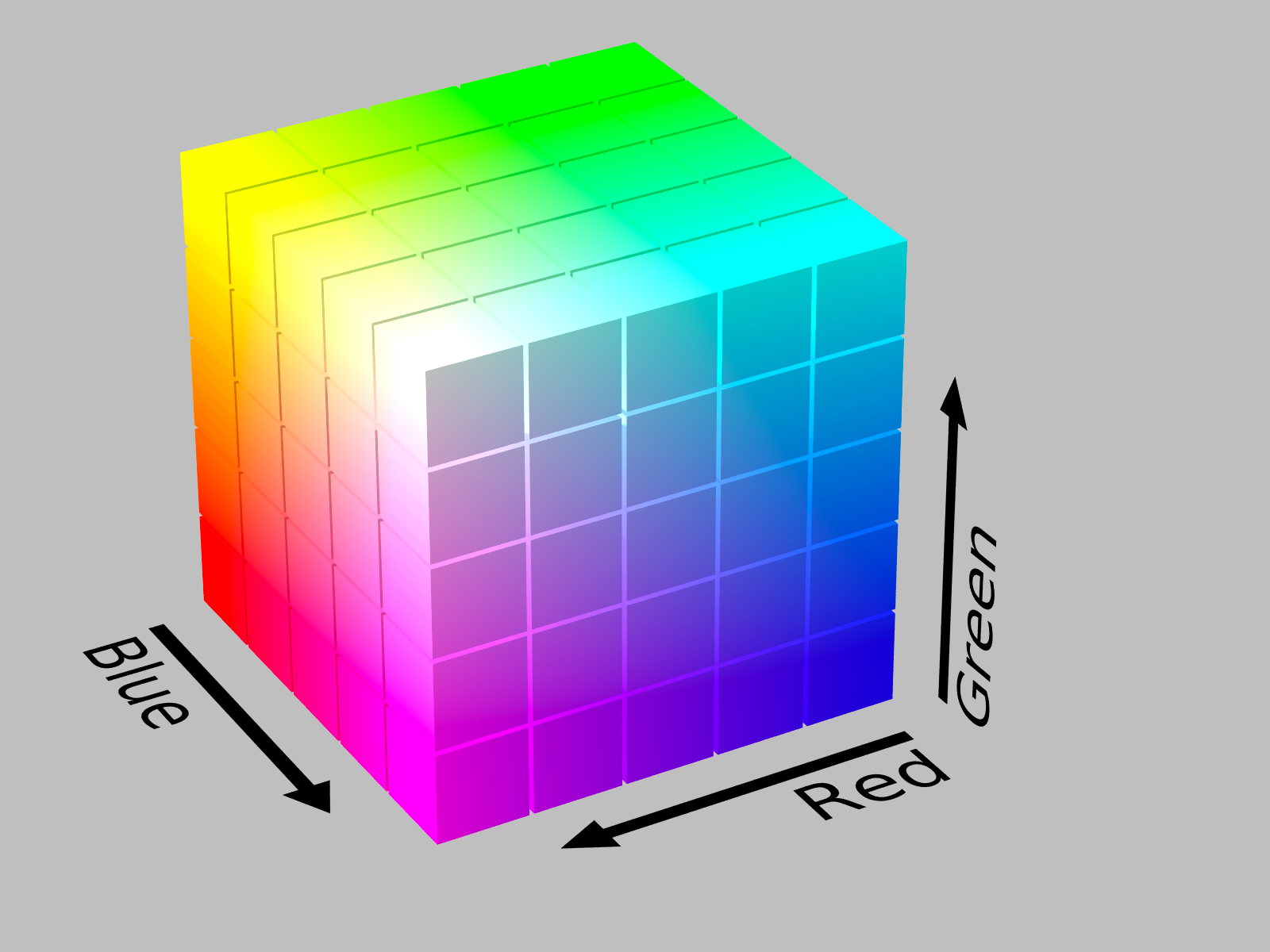
When we talk about a color's RGB values, we're essentially referencing its coordinates in this 3D space where each dimension can have values ranging from 0 (zero) to 255, totaling 256 values. The vector (R, G, B) is defined by three components: the intensity of Red (R), the intensity of Green (G), and the intensity of Blue (B). Each of these components typically ranges from 0 to 255, allowing for over 16 million, 16777216 to be exact, unique combinations, each representing a distinct color. For instance, the vector (255, 0, 0) signifies the full intensity of red with no contributions from green or blue, resulting in the color red.

Here are sample RGB values for some colors:

• Navy: (0, 0, 128)
• Turquoise: (64, 224, 208)
• Orange: (255, 165, 0)
• Green: (0, 128, 0) 
• Gray: (128, 128, 128)

The three values here can be seen as vectors representing a unique value in the color space containing 16777216 colors. Visualizing RGB values as vectors offers a profound advantage: the spatial proximity of two vectors gives a measure of color similarity. Colors that are close in appearance will have vectors that are close in the RGB space. This vector representation, therefore, not only provides a means to encode colors but also allows for an intuitive understanding of color relationships and similarities.

Similarity Searching

To find colors within an Euclidean distance of 1 from the color (148, 201, 44) in the RGB space, we vary each R, G, and B value by one up and one down to create the search space. This method will generate 3 x 3 x 3 = 27 color combinations but gives us a list of similar colors with specific distances. 

This is like identifying a small cube inside a larger RGB cube...

(147, 200, 43), (147, 200, 44), (147, 200, 45)

(147, 201, 43), (147, 201, 44), (147, 201, 45)

(147, 202, 43), (147, 202, 44), (147, 202, 45)

(148, 200, 43), (148, 200, 44), (148, 200, 45)

(148, 201, 43), (148, 201, 44)  <- This is the original color, (148, 201, 45)

(148, 202, 43), (148, 202, 44), (148, 202, 45)

(149, 200, 43), (149, 200, 44), (149, 200, 45)

(149, 201, 43), (149, 201, 44), (149, 201, 45)

(149, 202, 43), (149, 202, 44), (149, 202, 45)

All these 27 colors are similar to our original colors (148, 201, 44). This principle can be expanded to various distances and multiple ways to calculate the distance. If we were to store, index, and search RGBs in a database, let's see how this is done.

Hopefully, this gave you a good understanding of how the RGB models the color schemes and solves the similarity search problem.

Let's replace the RGB model with an LLM model and input text and images about tennis. We then search for "French open." Even though the input text or image didn't include "French open" directly, the effect of the similarity search is that Djokovic and the two tennis images will still be returned! That's the magic of the LLM model and vector search.

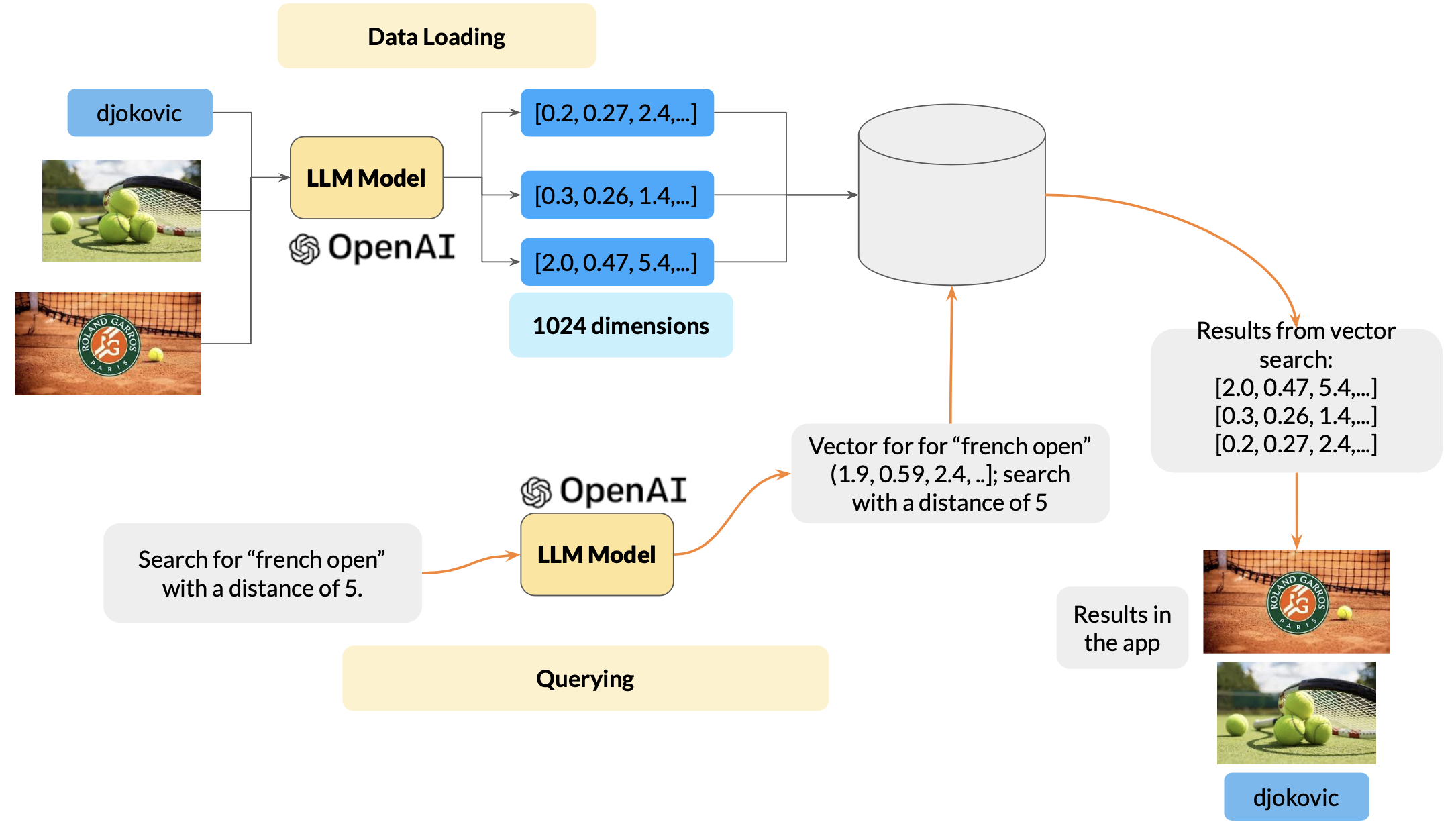
Vector indexing and vector search follow the same path. RGB encodes the 16 million colors in 3 bytes. But, the real-world data is more complicated. Languages, images, and videos much. more complicated. Hence, the vector databases use not three, but 300 or 3000 or more dimensions to encode data. Because of this, we need novel methods to store, index, and do similarity searches efficiently. However, the core principle is the same. More on how vector indexing and searching is done in a future blog!